16/MATH, TRIG, AND OTHER
FUNCTIONS
In addition to the simple math functions described earlier in this book, the MC-10 repertoire includes several advanced functions.
We'll give you a brief rundown of each function and show you how you can use it to perform any number of higher-level mathematical operations.
Before we do, however, there are a couple of functions and definitions you should be familiar with.
Note: Before the results of a math function can be displayed on the Screen, they must be prefaced by a PRINT statement.
Exponentiation (^)
Anytime you want to raise a number to the nth power, follow this format:
number ^ power
number specifies the number you wish to raise to power. It may be any numeric expression.
^ is generated by pressing [CONTROL][W].
power is the exponent to which number is raised. It may be any numeric expression. |
Exponentiation has precedence over other operators. For example, if you try -2^2, the result will be a negative number. To raise -2 to the 2nd power "correctly" (resulting in a positive number), enclose -2 in parentheses.
Start with a hard example-77 cubed. Try this:
PRINT 77 ^ 3 [ENTER]
and your Screen should display:
456533.002
OK
Try taking 10 to the 10th power and your Screen will display:
1.0000000e+10
OK
Since 10,000,000,000 has more than nine significant digits, the Computer went into E (scientific) notation.
How about 100 to the 100th power? This will produce an Overflow Error message. This means the answer was too big for the MC-10 to handle. The MC-10 was designed to handle any number from -10(to the)38th to 10(to the)38th.
The SQR Function
SQR enables you to find the square root of a number.
SQR (number)
number is a numeric expression not less than zero. |
For example, if you want the square root of 100, type:
PRINT SQR (100) [ENTER]
and you'll find out the answer is 10.
There Has To Be An Easier Way...
If you need to enter the SQR function without typing it in, press the key-combination of:
[CONTROL][?]
The ABS Function
ABS returns the absolute value of a number.
ABS (number)
number is a numeric expression. |
RUN this short program to see how it works:
10 INPUT "TYPE A NUMBER";N
20 PRINT "THE ABSOLUTE VALUE IS"; ABS(N)
30 END
There Has To Be An Easier Way...
If you need to enter the ABS function without typing it in, press the key-combination of:
[CONTROL][B]
The SGN Function
SGN tells you whether a number is positive, negative, or has a value of zero.
SGN (number)
number is a numeric expression. |
Try this short example:
10 INPUT "TYPE A NUMBER";X
20 IF SGN(X) = 1 THEN PRINT "POSITVE"
30 IF SGN(X) = 0 THEN PRINT "ZERO"
40 IF SGN(X) = -1 THEN PRINT "NEGATIVE"
50 END
There Has To Be An Easier Way...
If you need to enter the SGN function without typing it in, press the key-combination of:
[CONTROL][X]
The INT Function
The INT function tells the MC-10 to return the largest whole number not exceeding the given number.
INT (number)
number is a numeric expression. |
Try this short program to see INT at work:
10 INPUT "TYPE A NUMBER THAT HAS A DECIMAL
FRACTION";N
20 PRINT "THE WHOLE NUMBER PORTION OF ";N; "IS ";
INT(N)
30 END
There Has To Be An Easier Way...
If you need to enter the INT function without typing it in, press the key-combination of:
[CONTROL][C]
Trig Functions
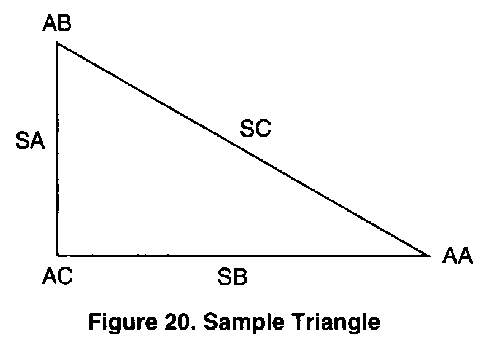
The trigonometry functions that Micro Color BASIC has have many practical applications. For instance, imagine the triangle you'll be working with in this chapter is actually the roof of a house you're building. These functions can help you determine either the length of the rafters or the slope of the roof. Notice we've labelled angles with the prefix A (angle A=AA, etc.). To distinguish between angles and sides, we've tagged the sides opposite their respective angles with the prefix S (for example, SA is opposite angle AA, etc.).
In trigonometry, SB is called "adjacent", side SA "opposite", and side SC "hypothenuse".
Using this triangle, we can define the common trig functions in the following manner:
Sine of AA=SIN(AA)=Opposite/Hypothenuse=SA/SC
Cosine of AA=COS(AA)=Adjacent/Hypothenuse=SB/SC
Tangent of AA TAN(AA)=Opposite/Adjacent=SA/SB
Degrees vs. Radians
To define an angle, you may use either of two units of measurement. While the most common unit is the degree, another "more technical" unit is the radian.
Your Computer assumes all angles are measured in radians. Since radians may be somewhat alien to you, you can convert them to degrees (and vice versa) this way:
| Degrees to Radians: |
Degrees/57.29577951 |
| Radians to Degrees: |
Radians*57.29577951 |
In the sample programs that follow, we've included a "converter". This allows you to input degrees and the Computer automatically converts them to radians (and vice versa for some purposes).
The SIN Function
The syntax for SIN is:
SIN (angle)
angle is a numeric expression for an angle in radians. |
One way to use SIN is to determine the two unknown sides of a triangle if two angles and the third side are known. Enter and run the following program. You can input whatever values you want:
5 CLS
10 INPUT "WHAT IS ANGLE A (AA)";AA : IF AA=< 0 OR
AA >= 180 THEN 100
20 INPUT "WHAT IS ANGLE B (AB)";AB : IF AB=< 0 OR
AB >= 180 THEN 100
30 INPUT "WHAT IS SIDE C (SC)";SC : IF SC =< 0
THEN 100
40 AC = 180 - (AA+AB) :REM VALUE OF ANGLE AC
50 IF (AA + AB + AC) < > 180 THEN 100
60 AA = AA/57.29577951: AB = AB/57.29577951:
AC = AC/57.29577951 :REM CONVERT DEGREES TO
RADIAN
70 SA = ((SIN (aa))/(SIN(AC)))*SC: IF SA < 0 THEN
100
80 SB = ((SIN (AB))/(SIN(AC))) * SC: IF SB < 0
THEN 100
90 PRINT "SIDE A (SA) IS" SA " LONG": PRINT "SIDE
B (SB) IS" SB " LONG.": GOTO 10
100 PRINT "SORRY, NOT A TRIANGLE. TRY AGAIN" :
GOTO 10
When the Computer prompts you for angles AB and AC, you should input the degrees-measures of the angles. If you try to use negative angles or angles greater than or equal to 180 degrees, the Computer will go to line 100, print the message, and re-prompt you. If you attempt to input a negative number for side SC, you'll have the same result.
Since you don't know the size of angle AC, the Computer automatically computes this in line 40. If the sum of the three angles is not equal to 180 degrees, the Computer takes appropriate action in line 50. Line 60 converts "your" degrees to the "Computer's" radians so the sine calculations may be done.
There Has To Be An Easier Way...
If you need to enter the SIN function without typing it in, press the key-combination of:
[CONTROL][N]
The COS Statement
The cosine function is related to the sine function and uses the following syntax:
COS (angle)
angle is a numeric expression for an angle in radians. |
One application of cosine is to determine the length of a triangles third side if you already know two sides and an angle. For angle and side identification, refer to the sample triangle.
5 CLS
10 INPUT "WHAT IS ANGLE C (AC)";AC : IF AC=< 0 OR
AC >= 180 THEN 100
20 AC = AC/57.29577951 :REM CONVERT DEGREES TO
RADIAN
30 INPUT "WHAT IS SIDE A (SA)";SA : IF SA =< 0 OR
THEN 100
40 INPUT "WHAT IS SIDE B (SB)";SB : IF SB =< 0
THEN 100
50 SC = ((SA ^ 2) + (SB ^ 2))-
(2*(SA*SB*COS(AC))): IF SC < 0 THEN 100
60 PRINT "SIDE C (SC) IS" SQR (SC)" LONG": GOTO 10
100 PRINT "SORRY, NOT A TRIANGLE. TRY AGAIN" :
GOTO 10
Notice the program works almost the same as the SIN program except for the use of exponentiation (^) in line 50 and SQR in line 60.
There Has To Be An Easier Way...
If you need to enter the COS function without typing it in, press the key-combination of:
[CONTROL][M]
The TAN Function
The third trigonometric function you can use with your MC-10 is TAN. This function allows you to calculate the tangent of an angle.
TAN (angle)
angle is a numeric expression for an angle in radians. |
Among other things, the tangent function can be used to determine the unknown length of one side of a triangle if you know the dimensions of another side and one angle.
5 CLS
10 INPUT "WHAT IS SIDE B (SB)"; SB : IF SB =< 0
THEN 100
20 INPUT "WHAT IS ANGLE A (AA)";AA : IF AA=< 0 OR
AA >= 180 THEN 100
30 AA = AA/57.29577951 :REM CONVERT DEGREES TO
RADIAN
40 SC = SB * (TAN (AA)): IF SC =< 0 THEN 100
50 PRINT "SIDE C (SC) IS" SC" LONG": GOTO 10
100 PRINT "SORRY, NOT A TRIANGLE. TRY AGAIN" :
GOTO 10
The key to this program, of course, is line 40, where the tangent of angle AA is multiplied by the length of side SB to determine the length of side SC.
There Has To Be An Easier Way...
If you need to enter the TAN function without typing it in, press the key-combination of:
[CONTROL][,]
The LOG Function
LOG returns the natural logarithm of a number. This is the inverse of EXP, so X=LOG(EXP(X)).
LOG (number)
number is a numeric expression greater than zero. |
The logarithm of a number is the power to which a given base must be raised to result in the number. Logs are useful in scientific and mathematical problems. In the LOG function, the base is e=2.718271828.
To find the logarithm of a number to another base B, use the formula log base B(x)=log e(x)/log e(B). For example, LOG(32758)/LOG(2) returns the logarithm to base 2 for 32768 (that is, the power to which 2 is raised to get 32768).
Try these:
PRINT LOG (1) [ENTER]
PRINT LOG (100) [ENTER]
PRINT LOG (2.718271828) [ENTER]
There Has To Be An Easier Way...
If you need to enter the LOG function without typing it in, press the key-combination of:
[CONTROL][.]
The VAL Function
The VAL function will convert a string value into a numeric value.
VAL (string)
string is a sting variable, constant, or expression. |
VAL accepts a string argument and evaluates it as a number. If the string characters don't make sense in a number, it returns a zero.
This function is useful for checking to see if answers are correct. How does it do this? RUN the following program to see:
10 X = RND(4)
20 Y = RND(4)
30 PRINT "WHAT IS "; X; "+"; Y
40 T = 0
50 A$ = INKEY$
60 T = T + 1
70 SOUND 128,1
80 IF T = 200 THEN 200
90 IF A$ = "" THEN 50
100 IF VAL(A$) = X + Y THEN 130
110 PRINT "WRONG"; X; "+"; Y; "="; X+Y
120 GOTO 10
130 PRINT "CORRECT"
140 GOTO 10
200 CLS 7
When you RUN this program. you'll have a few seconds to type in the answer to the arithmetic problem the Computer poses you with. Line 100 converts A$ into a numeric VALue. If A$ equals the string "5", VAL(A$) equals the number 5.
The EXP Function
The EXP function returns the natural exponential of a number, the e(raised to)number. This function is the inverse of LOG; therefore, X=EXP(LOG(X)).
EXP (number)
number is a numeric expression less than 88. |
RUN this program to see EXP at work.
10 CLS
20 INPUT "ENTER X"; X
30 PRINT "EXP(X)="; EXP (X)
40 GOTO 20
|
|